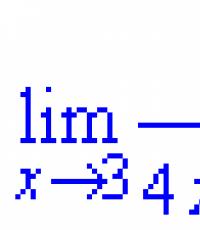Транскрипт

1 Лекция 4 ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ И ПЛОСКОСТИ Определение 1. Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90. Перпендикулярные прямые могут пересекаться, но могут быть и скрещивающимися. Определение 2. Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости. Определение 3. Две пересекающиеся плоскости называются взаимно перпендикулярными, если образованный ими двугранный угол равен 90. Теоремы о перпендикулярности прямых и плоскостей, доказываемые в школьном курсе геометрии , могут быть сформулированы в виде признаков перпендикулярности Признаки перпендикулярности прямых и плоскостей Признак 1. Прямая, перпендикулярная к одной из параллельных прямых, перпендикулярна к обеим параллельным прямым. t t" Пусть прямые a и b параллельны (рис. 4.1). Проведем перпендикуляр t к одной из прямых, например, к прямой a. Тогда прямая t будет перпендикулярна не только к прямой a, но и к прямой b. Из этого признака следует, что две взаимно перпендикулярные A прямые в пространстве не обязаны пересекаться. Они могут скрещиваться, но при этом быть взаимно перпендикулярны. Например, a b B на рис. 4.1 каждая из параллельных прямых t и t" перпендикулярна Рис. 4.1 каждой из прямых a и b. Признак 2. Если прямая t перпендикулярна каким-нибудь двум пересекающимся прямым, лежащим в плоскости Σ, то прямая t перпендикулярна к этой плоскости Σ (рис. 4.2). Две пересекающиеся прямые a и b определяют в пространстве некоторую плоскость Σ. Проведем перпендикуляр t к этим прямым (см. рис. 4.2). Согласно признаку 2, прямая t перпендикулярна к плоскости Σ. b a Σ t a Рис. 4.2 Рис. 4.3 Рис. 4.4 Признак 3. Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости (этот признак перпендикулярности следует непосредственно из определения 2). Дана плоскость Σ. Проведем к ней перпендикуляр t (рис. 4.3). Согласно признаку 3, прямая t перпендикулярна к произвольной прямой a, лежащей в плоскости Σ. Признак 4. Если плоскость Δ проходит через перпендикуляр к плоскости Σ, то плоскости Δ и Σ взаимно перпендикулярны (рис. 4.4). Σ t t Σ Δ 32

2 Дана плоскость Σ. Проведем к ней перпендикуляр t. Через прямую t проведем произвольную плоскость Δ (см. рис. 4.4). Согласно признаку 4, плоскость Δ перпендикулярна плоскости Σ. Признаки перпендикулярности используются при построении взаимно перпендикулярных прямых и плоскостей на комплексном чертеже Теорема 1 (о проекциях прямого угла) Если одна сторона прямого угла параллельна какой-либо плоскости проекций, а другая сторона является прямой общего положения, то прямой угол изображается на этой плоскости проекций прямым углом. Пусть отрезок AB перпендикулярен отрезку BC, причем отрезок AB горизонталь (AB П 1), а отрезок BC прямая общего положения (рис. 4.5). Докажем, что угол C 1 прямой, то есть C 1. Доказательство 1) Отрезок AB перпендикулярен отрезку BC по условию: AB BC. 2) Отрезок AB перпендикулярен линии связи B по построению. Следовательно (в соответствии с признаком 2 перпендикулярности прямой и плоскости), отрезок AB перпендикулярен плоскости Δ(BC B). 3) Проекция отрезка AB параллельна самому отрезку AB по условию. Отрезок AB перпендикулярен плоскости Δ, следовательно, проекция также перпендикулярна плоскости Δ. 4) Поскольку прямая перпендикулярна плоскости Δ, то она перпендикулярна прямой C 1, лежащей в плоскости Δ (признак 3). Следовательно, C 1. Теорема доказана. Следствие из теоремы 1. Если одна из взаимно перпендикулярных скрещивающихся прямых параллельна какой-либо плоскости проекций, то данные скрещивающиеся прямые изображаются на этой плоскости проекций прямым углом. Одну из сторон висящего в воздухе прямого угла ABC, показанного на рис. 4.5 (например, сторону BC), можно мысленно переместить в пространстве параллельно самой себе. Тогда прямая BC выйдет из пересечения со стороной AB. Но горизонтальные проекции прямых AB и BC все равно образуют прямой угол. Рассмотрим примеры построения комплексных чертежей взаимно перпендикулярных прямых. Задача 1. На чертеже дана горизонталь h и точка A (рис. 4.6). Требуется из точки A опустить перпендикуляр t на прямую h. Требование опустить перпендикуляр на прямую означает, что перпендикуляр к прямой должен с ней пересечься. В соответствии с теоремой 1, если прямая t перпендикулярна горизонтали h, то их горизонтальные проекции t 1 и должны быть взаимно перпендикулярны. Горизонталь h и прямая t, показанные на рис. 4.6, пересекаются в точке B и образуют прямой угол. Задача имеет единствен- 33 t 2 t 1 Рис. 4.6 A Рис º B Δ B1 C 1 C Рис. 4.7

3 ное решение, так как из точки A можно опустить единственный перпендикуляр на прямую h. Задача 2. Дана горизонталь h и точка M (рис. 4.7). Требуется через точку M провести прямую, перпендикулярную к горизонтали h, но не пересекающуюся с ней. Проведем через точку M какую-нибудь прямую m, горизонтальная проекция которой образует прямой угол с. В соответствии со следствием из теоремы 1, горизонталь h и прямая m перпендикулярны друг другу, но не пересекаются между собой (см. рис. 4.7). Задача имеет бесчисленное множество решений. Все прямые, проходящие через точку M и перпендикулярные к горизонтали h, образуют плоскость, перпендикулярную к h. Задача 3. Дана фронталь f и точка A (рис. 4.8). Требуется из точки A опустить перпендикуляр t на прямую f. Если прямая t перпендикулярна фронтали f, то, в соответствии с теоремой 1, их фронтальные проекции t 2 и должны быть взаимно перпендикулярны (см. рис. 4.8). Фронталь f и прямая t, показанные на чертеже, пересекаются в точке B и образуют прямой угол. Задача имеет единственное решение. Задача 4. Дана фронталь f и точка M (рис. 4.9). Требуется через точку M провести прямую, перпендикулярную к фронтали f, но не пересекающуюся с ней. Проведем через точку M какую-нибудь прямую m, фронтальная проекция которой образует прямой угол с. Фронталь f и прямая m, показанные на рис. 4.9, перпендикулярны друг другу (согласно следствию из теоремы 1), но между собой не пересекаются (скрещиваются). Задача имеет бесчисленное множество решений. На рис. 4.9 показано только одно из решений задачи Теорема 2 (о взаимной перпендикулярности прямых и плоскостей) Напомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к плоскости, то она перпендикулярна любой прямой в этой плоскости (см. п. 4.1). В частности, прямая, перпендикулярная к плоскости, перпендикулярна к главным линиям плоскости горизонтали и фронтали. Отсюда следует теорема об изображении на комплексном чертеже перпендикуляра к плоскости общего положения. Если прямая d перпендикулярна к плоскости, то на комплексном чертеже горизонтальная проекция d 1 прямой перпендикулярна горизонтальной проекции горизонтали (d 1), а фронтальная проекция d 2 прямой перпендикулярна фронтальной проекции фронтали (d 2), принадлежащим этой плоскости. Пусть прямая d перпендикулярна к плоскости общего положения Σ (рис. 4.10). Начертим в плоскости Σ ее d главные линии горизонталь h и фронталь f. Докажем, f что на комплексном чертеже проекции перпендикуляра d подчиняются условиям: d 1, d 2. Доказательство 1) Прямая d перпендикулярна плоскости Σ по условию. Следовательно, в соответствии с третьим призна- h ком перпендикулярности, прямая d перпендикулярна главным линиям плоскости Σ горизонтали h и фронтали f: d h, d f. Рис t 2 t 1 Рис. 4.8 Рис. 4.9

4 2) Прямые d и h образуют прямой угол, причем сторона h параллельна горизонтальной плоскости проекций. Следовательно, в соответствии с теоремой 1, горизонтальные проекции прямых d и h взаимно перпендикулярны: d 1. Первая часть теоремы доказана. 3) Прямые d и f также образуют прямой угол, причем сторона f параллельна фронтальной плоскости проекций. Следовательно, в соответствии с теоремой 1, фронтальные проекции прямых d и f взаимно перпендикулярны: d 2. Вторая часть теоремы, а вместе с тем и вся теорема, доказана. Запишем теорему 2 в символической форме. Если d Σ, то d 1, а d 2, где h и f - главные линии плоскости Σ. Рассмотрим примеры построения на чертеже взаимно перпендикулярных прямых и плоскостей во всех возможных сочетаниях. Таких сочетаний всего три: 1) взаимно перпендикулярные прямая и плоскость, 2) две взаимно перпендикулярные плоскости, 3) две взаимно перпендикулярные прямые Построение взаимно перпендикулярных прямой и плоскости Напомним утверждение теоремы 2. Плоскость Σ и прямая m взаимно перпендикулярны, если на чертеже выполнены условия:, где h и f главные линии плоскости Σ. Прямая задача. Через данную точку M провести прямую m, перпендикулярную к плоскости Σ общего положения. Плоскость Σ задана на чертеже прямыми a и b, пересекающимися в точке K (рис. 4.11). Δ 2 b 1 a K b 2 K D 2 D 1 Рис Рис Начертим главные линии плоскости Σ (горизонталь h и фронталь f). Для построения этих линий в плоскости Σ проведена произвольная вспомогательная прямая 1-2. На этой прямой отмечены точки 3 и 4, принадлежащие фронтали и горизонтали. Проведем через точку M прямую m таким образом, чтобы выполнить условия теоремы 2: горизонтальная проекция прямой m перпендикулярна к, а фронтальная проекция прямой m перпендикулярна к. Прямая m(,) перпендикулярна к плоскости Σ. Задача решена. 35

5 Обратная задача. Через точку D провести плоскость Δ, перпендикулярную прямой общего положения m (рис. 4.12). Плоскость, перпендикулярная к прямой общего положения, может быть задана пересекающимися горизонталью и фронталью, перпендикулярными к данной прямой. На рис через точку D проведены горизонталь h и фронталь f таким образом, чтобы выполнить условия: и. Задача решена. Действительно, в соответствии с теоремой 2, начерченная на рис плоскость Δ(h f) перпендикулярна прямой m. Прямая m перпендикулярна как горизонтали h, так и фронтали f Построение взаимно перпендикулярных плоскостей Плоскость, перпендикулярную к данной плоскости, можно провести двумя способами: либо через прямую, перпендикулярную данной плоскости, либо перпендикулярно прямой, принадлежащей заданной плоскости. Задача. Плоскость Σ общего положения задана пересекающимися прямыми a и b. Требуется через данную точку M провести плоскость Δ, перпендикулярную к плоскости Σ. n 2 Δ 2 l 2 Δ 2 a2 b a b b 1 b 1 n 1 l 1 Рис Рис Первый способ Начертим в плоскости Σ главные линии (горизонталь и фронталь), затем в соответствии с теоремой 2 проведем через точку M перпендикуляр m к плоскости Σ: и (рис. 4.13). Любая плоскость, проходящая через прямую m, перпендикулярна плоскости Σ. Проведем через точку M произвольную прямую n. Пересекающиеся прямые m и n определяют в пространстве плоскость Δ, перпендикулярную плоскости Σ. Имеется бесчисленное множество решений, так как через перпендикуляр к плоскости Σ можно провести бесчисленное множество плоскостей. Все они перпендикулярны плоскости Σ. Второй способ Проведем в плоскости Σ(a b) произвольную прямую l (рис. 4.14). Плоскость Δ, перпендикулярная к прямой l, задается пересекающимися горизонталью и фронталью. На рис через точку M проведены горизонталь h и фронталь f таким образом, чтобы выполнить условия теоремы 2 о перпендикулярности прямой и плоскости: l 1 и l 2. Плоскость Δ, заданная горизонталью h и фронталью f, перпендикулярна к прямой l. 36

6 Прямая l лежит в плоскости Σ, следовательно, плоскость Δ(h f) перпендикулярна к плоскости Σ. Имеется бесчисленное множество решений: плоскость, перпендикулярная любой прямой l в плоскости Σ, будет перпендикулярна к Σ Построение взаимно перпендикулярных прямых Напомним один из признаков перпендикулярности прямых и плоскостей: если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой в этой плоскости. Следовательно, для построения перпендикуляра к данной прямой m надо провести плоскость Σ, перпендикулярную к этой прямой. Любая прямая, лежащая в плоскости Σ, будет перпендикулярна прямой m. Задача. На чертеже (рис. 4.15) дана прямая m общего положения. Требуется через данную точку M провести прямую a, перпендикулярную прямой m. Через точку M проведем плоскость Σ, перпендикулярную прямой m. Плоскость Σ, перпендикулярная к прямой общего положения m, может быть задана пересекающимися горизонталью и фронталью, каждая из которых проводится перпендикулярно к прямой m. На рис через точку M проведены горизонталь h и фронталь f таким образом, чтобы выполнить условия: и. В соответствии с теоремой 2, начерченная на рис плоскость Σ, заданная горизонталью h и фронталью f, перпендикулярна прямой m. Любая прямая в плоскости Σ перпендикулярна прямой m. На чертеже показана только одна такая прямая (прямая a). Скрещивающиеся прямые общего положения m и a взаимно перпендикулярны. K 2 K 1 =Δ 2 Задача имеет множество решений: любая прямая в плоскости Σ, проходящая через точку M, перпендикулярна прямой m, то есть удовлетворяет условию задачи. Среди найденного множества прямых, проходящих через точку M, есть единственная прямая, которая не только перпендикулярна к прямой m, но и пересекается с ней. Как построить такую прямую? Эта задача будет рассмотрена в следующем параграфе Решение типовых задач Рассмотрим несколько геометрических задач, в которых Σ требуется выполнять на чертеже построение взаимно перпендикулярных прямых и плоскостей. 1 Задача 1. Опустить перпендикуляр из точки M на прямую m общего положения (рис. 4.16). Через точку M проведем плоскость Σ, перпендикулярную Рис прямой m. Зададим эту плоскость горизонталью и фронталью так, чтобы на чертеже выполнялись условия теоремы 2: и. Все прямые в плоскости Σ перпендикулярны прямой m. 37 a Рис. 4.15

7 Найдем точку K пересечения прямой m с плоскостью Σ. Для построения точки K следует применить схему решения первой позиционной задачи: провести через m вспомогательную секущую плоскость Δ, построить линию разреза 1-2 и отметить искомую точку K=m (1-2). Прямая MK лежит в плоскости Σ, следовательно, она перпендикулярна прямой m. При этом прямая MK пересекает прямую m. Поэтому отрезок MK есть искомый перпендикуляр, опущенный из точки M на прямую m. " Рис " Задача 2. Найти расстояние от точки M до прямой m. Искомое расстояние равно длине перпендикуляра, опущенного из точки M на прямую m. Поэтому сначала надо опустить перпендикуляр MK на прямую m (см. рис. 4.16), а затем определить истинную длину отрезка MK способом прямоугольного треугольника (см. п). Задача 3. Построить ортогональную проекцию точки M на плоскость Σ общего положения (рис. 4.17). Для построения ортогональной проекции надо через точку M провести проецирующий луч m, перпендикулярный плоскости Σ. Точка пересечения M" этого луча с плоскостью Σ ортогональная проекция точки M на плоскость Σ. Чтобы начертить прямую m, перпендикулярную плоскости Σ, надо выполнить условия: и, где h и f главные линии плоскости Σ (теорема 2). После построения перпендикуляра m находим точку M" пересечения этого перпендикуляра m с плоскостью Σ, используя вспомогательную секущую плоскость Δ (первая позиционная задача, см. лекцию 3). Точка M" искомая ортогональная проекция. Задача 4. Найти расстояние от точки M до плоскости Σ. Искомое расстояние равно длине перпендикуляра, опущенного из точки на плоскость. Поэтому сначала надо опустить перпендикуляр MM" из точки M на плоскость Σ (см. рис. 4.17), затем определить истинную длину отрезка MM" способом прямоугольного треугольника (см. п). Задача 5. Построить ортогональную проекцию отрезка AB на плоскость Σ, заданную горизонталью и фронталью (рис. 4.18). Чтобы найти ортогональные проекции A", B" концов отрезка AB на плоскость Σ, проведем через точки A и B перпендикуляры к плоскости Σ (теорема 2). Затем найдем точки A", B" пересечения этих перпендикуляров с плоскостью Σ (первая позиционная задача). Отрезок A"B" искомая ортогональная проекция данного отрезка AB на плоскость Σ. Если задача решена правильно, то ортогональная проекция A"B" пройдет через точку K пересечения прямой AB с плоскостью Σ (см. рис. 4.18). A" 2 K 2 B" 2 A" 1 K 1 B" 1 Рис

8 Задача 6. Построить ортогональную проекцию треугольника ABC на плоскость параллелограмма (рис. 4.19). K 2 K 1 A" 2 A" 1 A1 B" 2 Рис E 2 D 2 E 1 B" 1 C 2 D 1 C 1 C" 2 C" 1 Для решения задачи надо построить ортогональные проекции сторон треугольника на плоскость параллелограмма (так же, как и в предыдущей задаче). Ортогональная проекция какой-либо стороны треугольника на плоскость параллелограмма проходит через точку пересечения этой стороны с плоскостью параллелограмма. Например, в точке E сторона AB треугольника пересекается с плоскостью параллелограмма. Ортогональная проекция A"B" стороны AB проходит через точку E. Аналогичным образом, ортогональная проекция B"C" стороны BC проходит через точку D пересечения стороны BC с плоскостью параллелограмма. Точки D и E находят по схеме решения первой позиционной задачи. Вспомогательные построения на рис условно не показаны. Задача 7. Построить множество точек, удаленных от плоскости Σ(ABC) на расстояние 30 мм (рис. 4.20). Множество точек, удаленных от данной плоскости на заданное расстояние, расположено в плоскости Σ", параллельной данной плоскости Σ и удаленной от нее на заданное расстояние. n 1 n 2 R 0 Δz Δz R 2 R 1 A" 2 L 2 N 2 N 1 30 мм A" 1 L 1 Σ" 1 Σ" 2 Рис C 2 C 1 Восставим перпендикуляр n к плоскости Σ из любой точки этой плоскости (например, из точки A). Для этого в плоскости Σ начертим ее главные линии (горизонталь и фронталь) и начертим проекции перпендикуляра n в соответствии с условиями теоремы 2 (n 1 и n 2). Отложим вдоль перпендикуляра n от точки A отрезок AA" длиной 30 мм (см. п). Через точку A" проведем плоскость Σ", параллельную плоскости Σ. На рис плоскость Σ" задана парой пересекающихся прямых, параллельных сторонам треугольника ABC. Задача решена. Задача имеет два решения. Второе решение будет получено, если заданное расстояние 30 мм отложить вдоль перпендикуляра n в другую сторону от точки A. Задача 8. Построить множество точек, равноудаленных от данных точек A и B (рис. 4.21). Точки, одинаково удаленные от двух данных точек A и B, располагаются в плоскости Σ, перпендикулярной к отрезку AB и проходящей через его середину. Искомую плоскость Σ зададим горизонталью и фронталью, перпендикулярными к отрезку AB и проходящими через его середину (точка O на рис. 4.21). Согласно теореме о перпендикулярности прямой и плоскости, на чертеже должны быть выполнены условия: 39

9 , где h и f главные линии искомой плоскости Σ, перпендикулярной отрезку AB. Поскольку плоскость Σ(h f) перпендикулярна к отрезку AB и проходит через O 2 O 1 Рис h2 его середину, то все точки плоскости Σ равноудалены от данных точек A и B. Задача решена. Задача 9. Определить расстояние между двумя параллельными прямыми a и b (рис. 4.22). Отметим на одной из параллельных прямых (например, на прямой a) произвольную точку A. Из точки A опустим перпендикуляр AB на прямую b (см. задачу 1). Расстояние между параллельными прямыми равно длине отрезка AB. Составим схему решения задачи. Действие 1. Опускаем перпендикуляр AB из точки A на прямую b. Для этого проводим через точку A плоскость Θ, перпендикулярную прямым a и b (теорема 2). Затем с помощью проведенной через b вспомогательной секущей плоскости Σ находим точку B пересечения прямой b с плоскостью Θ (первая позиционная задача). Действие 2. Способом прямоугольного треугольника (см. п) определяем истинную длину отрезка AB. Задача решена. Θ 2 b 2 f2 Θ 1 Рис a 2 A 0 Δz b 1 AB Δz Вопросы для повторения 1. Сформулировать признаки перпендикулярности прямой и плоскости, двух плоскостей. 2. Могут ли скрещивающиеся прямые быть взаимно перпендикулярны? 3. Сформулировать условие, при котором две прямые, расположенные в пространстве перпендикулярно друг другу, изображаются на плоскости проекций П 1 или П 2 взаимно перпендикулярными прямыми (теорема 1 о проекциях прямого угла). 4. Сколько прямых, перпендикулярных к данной прямой, можно провести через данную точку пространства? 5. Cколько перпендикуляров можно опустить из данной точки пространства на данную прямую? 6. Как изображается на чертеже прямая линия, перпендикулярная к данной плоскости (теорема 2 о проекциях прямой, перпендикулярной к плоскости)? 7. Сколько перпендикуляров к плоскости можно провести через данную точку пространства? 8. Сколько плоскостей, перпендикулярных к данной плоскости, можно провести через данную точку пространства? 40

Лекция 12 КОМБИНИРОВАННЫЕ ЗАДАЧИ Многие задачи начертательной геометрии сводятся к построению фигур (точек, линий, поверхностей), удовлетворяющих определенным позиционным или метрическим условиям. Каждому

ЛЕКЦИЯ 3. 3. ПОЗИЦИОННЫЕ ЗАДАЧИ Позиционными называют задачи, связанные с определением взаимного расположения геометрических фигур. Обычно в этих задачах определяется взаимная принадлежность фигур или

Лекция 5 СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА Решение многих геометрических задач (как метрических, так и позиционных) упрощается, если исходные фигуры занимают частное положение относительно плоскостей проекций.

ЛЕКЦИЯ 2 (ПРОДОЛЖЕНИЕ ТЕМЫ «КОМПЛЕКСНЫЙ ЧЕРТЕЖ») 2.3. ПЛОСКОСТЬ 2.3.1. ЗАДАНИЕ ПЛОСКОСТИ НА ЧЕРТЕЖЕ Любую плоскость определяют (рис. 2.14): а) три точки, не лежащие на одной прямой (A,B,C); б) прямая и

5. ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ И ПРЯМЫЕ 5.1. Прямая линия, перпендикулярная плоскости 5.. Взаимно перпендикулярные плоскости 5.3. Взаимно перпендикулярные прямые 5.1. Прямая линия, перпендикулярная

Б 1. Предмет начертательной геометрии (Н.Г.) Н.Г. математическая наука. Это тот раздел геометрии, который изучает теоретические основы построения плоских изображений пространственных фигур и способы графического

Лекция 3 ПОЗИЦИОННЫЕ ЗАДАЧИ Позиционными задачами называют задачи, в которых надо определить общие элементы геометрических фигур, заданных на чертеже. В начертательной геометрии рассматривают две позиционные

ЛЕКЦИЯ 2 Условные обозначения, сокращения и знаки. Предмет изучения начертательной геометрии. Геометрические образы. Метод проецирования. Виды проецирования. Образование комплексного чертежа. Комплексные

МОДУЛЬ 9 «Теоретические основы стереометрии» 1. Вопросы стереометрии и простейшие следствия. 2. Параллельность прямых и плоскостей. 3. Перпендикулярность прямых и плоскостей. 1. Вопросы стереометрии и

Занятие 1 Точка. Прямая. Положение прямой относительно плоскостей проекций. Взаимное положение прямых. Принадлежность точки прямой. 1.1 Свойства параллельного проецирования Рис. 1.1 Свойства параллельного

Лекция 2 ЧЕРТЕЖИ ПРОСТЕЙШИХ ГЕОМЕТРИЧЕСКИХ ФИГУР В 1784 году английский изобретатель Дж. Уатт разработал и запатентовал первую универсальную паровую машину. С небольшими усовершенствованиями она более

ЛЕКЦИЯ 3 ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ Задачи, связанные с определением взаимного расположения геометрических элементов (прямых и плоскостей), называются позиционными. Обычно в

92 ГЛАВА 2. СЕМЕСТР: ВЕСНА 2015 Заметим, что неравенства будут верны и при π < x < 0, так как все входящие 2 в неравенство функции четные. Устремим x 0 и воспользуемся теоремой 24 (о двух милиционерах

ПРЯМАЯ ЛИНИЯ НА ЭПЮРЕ МОНЖА.. Задание прямой.. Прямые общего положения.3. Прямые частного положения.4. Принадлежность точки прямой. Деление отрезка прямой линии в данном отношении.5. Определение длины

ОСНОВЫ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ Начертательная геометрия наука, изучающая способы построения изображений пространственных фигур на плоскости. Наиболее простым и удобным является проецирование на взаимно

ЛЕКЦИЯ 5 5. СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА Решение пространственных задач на комплексном чертеже значительно упрощается, если интересующие нас элементы фигуры занимают частное положение. Переход

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «НИЖЕГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Графическая работа 3 Пример выполнения листа 4 Содержание четвёртого листа работы. Даны плоскость треугольника ABC и точка D. Требуется: 1. Определить расстояние от точки D до плоскости, заданной треугольником

3. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫ. ПЛОСКОСТЬ 3.. Взаимное положение прямых 3.2. Проекции плоских углов 3.3. Изображение плоскости на чертеже 3.4. Прямая и точка в плоскости 3.5. Главные линии плоскости 3.6.

Лекция 1 Методы проекций. Комплексный чертеж точки, прямой, плоскости. 1.1 Центральное и параллельное (прямоугольное) проецирование. Основные свойства прямоугольного проецирования. 1.2 Чертеж точки. 1.3

Начертательная геометрия: конспект лекций Юлия Щербакова 2 3 И. С. Козлова, Ю. В. Щербакова Начертательная геометрия. Конспект лекций 4 Лекция 1. Сведения о проекциях 5 1. Понятие проекций Начертательной

4. ПРЯМАЯ И ПЛОСКОСТЬ. ДВЕ ПЛОСКОСТИ 4.. Прямая линия, параллельная плоскости 4.. Прямая линия, пересекающаяся с плоскостью частного положения 4.3. Пересечение плоскости частного положения с плоскостью

10.1. Âàêóóìíûå äèîäû 11 Ãëàâà 1 åðòåæè ýëåìåíòàðíûõ ãåîìåòðè åñêèõ îáúåêòîâ В настоящей главе под элементарными геометрическими объектами будем понимать такие объекты, как точка, прямая, плоскость и плоская

Чертеж точки Чертеж в системе прямоугольных проекций образуется при проецировании геометрического образа на две либо три взаимно перпендикулярных плоскости: горизонтальную плоскость H, фронтальную V и

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра начертательной геометрии и графики Начертательная геометрия Плоскости Методические указания и задания для

Аксиомы стереометрии 1. 2. 3. 4. 5. Следствия из аксиом 1. 2. Всегда ли верно утверждение? 1. Любые 3 точки лежат в одной плоскости. 1 2. Любые 4 точки лежат в одной плоскости. 3. Любые 3 точки не лежат

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ "ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ - УЧЕБНО-НАУЧНО- ПРОИЗВОДСТВЕННЫЙ КОМПЛЕКС" ФАКУЛЬТЕТ НОВЫХ ТЕХНОЛОГИЙ

Аналитическая геометрия Аналитическая геометрия раздел геометрии, в котором простейшие линии и поверхности (прямые, плоскости, кривые и поверхности второго порядка) исследуются средствами алгебры. Линией

ЛЕКЦИЯ 7 7. МНОГОГРАННИКИ. ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ С ПЛОСКОСТЬЮ И ПРЯМОЙ. Гранные поверхности это поверхности, образованные перемещением прямолинейной образующей по ломаной линии. Часть этих поверхностей

Перпендикулярность плоскостей Две пересекающиеся плоскости называются перпендикулярными, если какая-либо плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным

Лекция 11 ПЛОСКОСТЬ, КАСАТЕЛЬНАЯ К ПОВЕРХНОСТИ Первоначальное понятие о касающихся друг друга линиях или поверхностях мы приобретаем из повседневного опыта. Например, интуитивно ясно, что лежащие на столе

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Национальный исследовательский ядерный университет

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ Кафедра начертательной геометрии и графики И.Г. Хармац НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Пособие по подготовке к блочной аттестации и выполнению

Вопросы к блоку 1 спец. 230101 Введение. Предмет начертательной геометрии. Метод проецирования. Комплексный чертеж Монжа. Центральное (коническое) проецирование. Параллельное (Цилиндрическое) проецирование.

ЛЕКЦИЯ Глава 3. ПЛОСКОСТЬ 3.. Задание плоскости на чертеже. Следы плоскости Плоскостью называется поверхность, образуемая перемещением прямой линии, которая движется параллельно самой себе по неподвижной

Развертки поверхностей Разверткой поверхности называется плоская фигура, полученная в результате совмещения всех точек поверхности с одной плоскостью. Между поверхностью и ее разверткой устанавливается

3. Прямая в пространстве. Уравнения прямой в пространстве Пусть A +B +C +D =0 и A +B +C +D =0 уравнения любых двух различных плоскостей содержащих прямую l. Тогда координаты любой точки прямой l удовлетворяют

Annotation Данное учебное пособие представляет собой курс лекций и предназначено для студентов, сдающих экзамен по специальности «Начертательная геометрия». Подготовлено с учетом требований Министерства

Глава 1: Теоретические основы проецирования геометрических фигур на плоскость 1.1 Обозначения и символы 1. Точки заглавными буквами латинского алфавита: A, B, C, D, E, ; линии строчными буквами латинского

1. Изображение плоскости. Способы задания плоскостей. Плоскость есть такое множество точек, основные свойства которого выражаются следующими аксиомами: Через три точки, не принадлежащие одной прямой, проходит

ПРЯМОЙ ЦИЛИНДР Пусть в пространстве заданы две параллельные плоскости и. F круг в одной из этих плоскостей, например. Рассмотрим ортогональное проектирование на плоскость. Проекцией круга F будет круг

Плоскость. Общее уравнение плоскости и его исследование ЗАДАЧА. Записать уравнение плоскости, проходящей через точку M (; ;), перпендикулярно вектору N = {A; B; C}. Вектор, перпендикулярный плоскости,

КОНСПЕКТ ЛЕКЦИЙ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ Преподаватель Студент Группа 1 ПРЕДМЕТ И МЕТОД НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ Начертательная геометрия это один из разделов геометрии, изучающий методы изображения

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ЮЖНО-УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ В.А. Короткий, Л.И. Хмарова, Е.А. Усманова НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Решение задач Челябинск 2016 Министерство

МИНИСТЕРСТВО ТРАНСПОРТА РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ Кафедра начертательной

Лекция 7 ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ И С ПРЯМОЙ ЛИНИЕЙ В предыдущих лекциях рассматривались чертежи простейших геометрических фигур (точек, прямых, плоскостей) и произвольных кривых линий и поверхностей,

Глава 7 ОСНОВНЫЕ ПОНЯТИЯ СТЕРЕОМЕТРИИ 7.1. ПАРАЛЛЕЛЬНОСТЬ В СТЕРЕОМЕТРИИ 7.1.1. Аксиомы стереометрии (наличие четырех точек не на плоскости, принадлежность прямой B к плоскости, плоскость через три точки

Федеральное агентство по образованию РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ НЕФТИ И ГАЗА им. И.М. ГУБКИНА А.В. Бочарова, Т.П. Коротаева ИНЖЕНЕРНАЯ ГРАФИКА Точка, прямая плоскость на комплексном чертеже

И. С. Козлова, Ю. В. Щербакова НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ. ЭКЗАМЕН В КАРМАНЕ Публикуется с разрешения правообладателя Литературного агентства «Научная книга» Лекция 1. Сведения о проекциях 1. Понятие проекций

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Тестовые задания 7 вариант Хабаровск 2014 0 Тема 1.Точка 1. Указать правильный ответ Ось проекций 0У это 1 линия пересечения плоскостей П 1 и П 2 2 линия пересечения плоскостей

Линейная алгебра и аналитическая геометрия Тема: Плоскость Лектор Пахомова Е.Г. г. 3. Плоскость. Общее уравнение плоскости и его исследование ЗАДАЧА. Записать уравнение плоскости, проходящей через точку

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА Уральский ргосударственный университет путей сообщения Тюменский филиал Кафедра графики Фадеев В.П. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Екатеринбург 2006 ФЕДЕРАЛЬНОЕ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ВОЛОГОДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра начертательной геометрии и графики НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ. ИНЖЕНЕРГАЯ ГРАФИКА Методические указания и

ЛЕКЦИЯ N3. Поверхности и линии в пространстве и на плоскости. Прямая на плоскости..уравнение прямой с угловым коэффициентом.....общее уравнение прямой.... 3.Угол между двумя прямыми. Условия параллельности

Министерство образования и науки Российской Федерации Саратовский государственный технический университет РЕШЕНИЕ МЕТРИЧЕСКИХ ЗАДАЧ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ Методические указания к практическим занятиям

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Тестовые задания 5 вариант Хабаровск 2014 0 Тема 1. Точка 1. Указать правильный ответ Плоскость проекций П 1 называется 1 горизонтальная плоскость проекций 2 фронтальная плоскость

Практическое занятие 1 Тема: Гипербола План 1 Определение и каноническое уравнение гиперболы Геометрические свойства гиперболы Взаимное расположение гиперболы и прямой, проходящей через ее центр Асимптоты

ПРЕДМЕТ И МЕТОД Начертательная геометрия и инженерная графика 1 Основным методом построения изображений на плоскости является метод проекций. Проекция Проецирование ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ ПАРАЛЛЕЛЬНОЕ

1 вариант Определите, является ли утверждение верным (ответьте «да» или «нет») 1 Через любые три точки проходит ровно одна прямая. 2 Через любую точку проходит более одной прямой. 3 Любые три прямые имеют

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Хабаровский государственный технический университет» ПЛОЩАДКА В ОРТОГОНАЛЬНЫХ ПРОЕКЦИЯХ

ЛИНЕЙНАЯ АЛГЕБРА Лекция Прямая и плоскость в пространстве Содержание: Уравнение плоскости Взаимное расположение плоскостей Векторно-параметрическое уравнение прямой Уравнения прямой по двум точкам Прямая

7. СПОСОБЫ ПРЕОБРАЗОВАНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА 7.1. Метод замены плоскостей проекций 7.2. Метод вращения вокруг оси, перпендикулярной к плоскости проекций 7.1. Метод замены плоскостей проекций При решении

Список вопросов и заданий для подготовки к вступительному испытанию по геометрии Если абитуриент учится по учебнику Погорелова А.В.: I. Основные свойства простейших геометрических фигур: 1. Приведите примеры

Министерство образования и науки Российской Федерации Федеральное агентство по образованию Саратовский государственный технический университет РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ Методические

Аналитическая геометрия в пространстве Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию Прямоугольная система координат Охy в пространстве

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ Тестовые задания 4 вариант Хабаровск 2014 0 Тема 1. Точка 1. Указать правильный ответ Ось проекций 0Z - это 1 линия пересечения плоскостей П 1 и П 2 2 линия пересечения плоскостей

Обратимость чертежа, т. е. однозначное определение положения точки в пространстве по ее проекциям, может быть обеспечена проецированием на две непараллельные плоскости проекций.

Для удобства проецирования в качестве двух плоскостей проекций выбирают две взаимно перпендикулярные плоскости (рис. 1.11). Одну из них принято располагать горизонтально – ее называют горизонтальной плоскостью проекций , другую – вертикально, параллельно плоскости чертежа. Такую вертикальную плоскость называют фронтальной плоскостью проекций . Эти плоскости проекций пересекаются по линии, называемой осью проекций .

Ось проекций разделяет каждую из плоскостей проекций на две полуплоскости, или полы.

Обозначим плоскости проекций: π2 – фронтальную, π, – горизонтальную, ось проекций – буквой x или в виде дроби π2/ π1 . Плоскости проекций π2 и π, образуют систему π2, π,.

Плоскости проекций, пересекаясь, образуют четыре двугранных угла, из которых приведенный на рис. 1.11 (с обозначениями граней π2, π1) считают первым.

В промышленности чертежи многих деталей выполняют также в системе двух взаимно перпендикулярных плоскостей, пересекающихся по вертикальной оси проекций ζ (рис. 1.12). При этом фронтальной плоскостью проекций оставляют также плоскость π2, а перпендикулярную ей и обозначаемую π3, называют .

В системе двух взаимно перпендикулярных плоскостей проекций: горизонтальной проекцией точки называют прямоугольную проекцию точки на горизонтальной плоскости проекций;

фронтальной проекцией точки называют прямоугольную проекцию точки на фронтальной плоскости проекций.

Наглядное изображение построения проекций произвольной точки А в системе π2, π, показано на рис. 1.13. Горизонтальную проекцию, обозначенную А ", находят как пересечение перпендикуляра, проведенного из точки А к плоскости π, с этой плоскостью. Фронтальную проекцию, обозначенную А ", находят как пересечение перпендикуляра, проведенного из точки А к плоскости π2, с этой плоскостью.

Проецирующие прямые ΑΑ " и ΑΑ перпендикулярные к плоскостям π2 и π, принадлежат плоскости α. Она перпендикулярна плоскостям проекций и пересекает ось проекций в точке Α χ. Три взаимно перпендикулярные плоскости α, π2 и π, пересекаются по взаимно перпендикулярным прямым, τ. е. прямые А "Α χ, А Ά χ и ось χ взаимно перпендикулярны.

Построение некоторой точки А в пространстве по двум заданным ее проекциям – фронтальной А " и горизонтальной А " – показано на рис. 1.14. Точку А находят в пересечении перпендикуляров, прове-

денных из проекции А” к плоскости π2 и из проекции А " к плоскости π,. Проведенные перпендикуляры принадлежат одной плоскости α, перпендикулярной плоскостям π2 и π, и пересекаются в единственной искомой точке А пространства.

Таким образом, две прямоугольные проекции точки вполне определяют ее положение в пространстве относительно данной системы взаимно перпендикулярных плоскостей проекций.

Рассмотренное наглядное изображение точки в системе π2, π, для целей черчения неудобно ввиду сложности. Преобразуем его так, чтобы горизонтальная плоскость проекций совпала с фронтальной плоскостью проекций, образуя одну плоскость чертежа. Это преобразование осуществляют (рис. 1.15) путем поворота вокруг оси χ плоскости π, на угол 90° вниз. При этом отрезки Α χ А " и Α χ А " образуют один отрезок А "А расположенный на одном перпендикуляре к оси проекции – на линии связи. В результате указанного совмещения плоскостей π2 и πι получается чертеж – рис. 1.16, известный под названием эпюр или эпюр Монжа . Это чертеж в системе π2, π, (или в системе двух прямоугольных проекций). Без обозначения плоскостей π2 и π, этот чертеж приведен на рис. 1.17.

Гаспар Монж (1746–1818) – французский ученый, общественный и государственный деятель в период французской революции 1789–1794 гг. и правления Наполеона 1 . Накапливавшиеся с древних времен сведения и приемы изображения пространственных форм на плоскости были приведены в систему и развиты в труде Г. Монжа, изданном в 1799 г. под названием Geometric descriptive (русский перевод (13)).

Начертательную геометрию в России начали преподаватьс 1810 г. Первые труды по ней опубликованы К.И. Потье (1816) и Я.А. Севастьяновым (1821). Большой вклад в развитие начертательной геометрии внесли многие русские и советские ученые (более подробные сведения приведены в книгах , , и др.).

Проецирование на три взаимно перпендикулярные плоскости проекций

В зависимости от сложности для полного выявления наружных и внутренних форм деталей и их соединений и для решения ряда задач бывают необходимы три и более изображений. Поэтому вводят три и более плоскостей проекций.

Введем в систему π2, π, третью вертикальную плоскость проекций (рис. 1.18), перпендикулярную оси χ и соответственно фронтальной и горизонтальной плокостям проекций. Ее называют профильной плоскостью проекций и обозначают π2 (см. также рис. 1.12). Такую систему плоскостей проекций называют системой π2, π, π3. В этой системе оси проекций ζ и у являются линиями пересечения профильной плоскости проекций с фронтальной и горизонтальной. Точка О – пересечение всех трех осей проекций.

Схема совмещения трех взаимно перпендикулярных плоскостей проекций в одну плоскость чертежа показана на рис. 1.19. При этом ось у занимает два положения.

Наглядное изображение некоторой точки А, ее проекций А ", А А в системе π2, щ, π }, а также их координат приведены на рис. 1.20, ее чертеж – на рис. 1.21.

Профильной проекцией точки называется прямоугольная проекция точки на профильной плоскости проекций (например, проекция А"" на рис. 1.21).

Фронтальная и профильная проекции точки (А" и А "") лежат на одной линии связи (А " А перпендикулярной оси ζ-

Профильную проекцию точки строят несколькими способами (рис. 1.21).

Через фронтальную проекцию проводят линию связи, перпендикулярную оси ζ, и от оси г отмечают координату у а (отрезок/1 Ά χ).

Это построение можно выполнить также с помощью дуги окружности, проведенной из центра О, или с помощью прямой, проведенной под углом 45° к оси у. Первый из указанных способов предпочтителен, как более точный.

• Наряду с указанными обозначениями плоскостей проекций в литературе применяют и другие обозначения, например буквами V, Η, W.
• Бриге (франц.) – чертеж, проект.

Существует множество деталей, информацию о форме кото­рых невозможно передать двумя проекциями чертежа (рис. 75).

Для того чтобы информация о сложной форме детали была представлена достаточно полно, используют проецирование на три взаимно перпендикулярные плоскости проекции: фронталь­ную - V, горизонтальную - H и профильную - W (читается «дубль вэ»).

Система плоскостей проекций представляет собой трехгран­ный угол с вершиной в точке О. Пересечения плоскостей трех­гранного угла образуют прямые линии - оси проекций (OX, OY, OZ) (рис. 76).

В трехгранный угол помещают предмет так, чтобы его формо­образующая грань и основание были бы параллельны соответст­венно фронтальной и горизонтальной плоскостям проекций. За­тем через все точки предмета проводят проецирующие лучи, перпендикулярные всем трем плоскостям проекций, на которых получают фронтальную, горизонтальную и профильную проекции предмета. После проецирования предмет удаляют из трехгран­ного угла, а затем горизонтальную и профильную плоскости про­екций поворачивают на 90* соответственно вокруг осей ОХ и OZ до совмещения с фронтальной плоскостью проекции и получают чертеж детали, содержащий три проекции.

Рис. 75. Проецирование на две плоскости проекций не всегда дает
полное представление о форме предмета

Рис. 76. Проецирование на три взаимно перпендикулярные
плоскости проекций

Три проекции чертежа взаимосвязаны друг с другом. Фрон­тальная и горизонтальная проекции сохраняют проекционную связь изображений, т. е. устанавливаются проекционные связи и между фронтальной и горизонтальной, фронтальной и профиль­ной, а также горизонтальной и профильной проекциями (см. рис. 76). Линии проекционной связи определяют местоположение каждой проекции на поле чертежа.

Во миогнх странах мира принята другая система прямо- угольного проецирования на три взаимно перпендикулярные плоскости проекций, которая условно называется «амери­канская» (см. Приложение 3). Основное eе отличие состоит в том, что по-иному, относительно проецируемого объекта, в пространстве располагается трехгранный угол и в других направлениях разворачива­ются плоскости проекций. Поэтому горизонтальная проекция оказывается над фронтальной, а профильная проекция - справа от фронтальной.

Форма большинства предметов представляет собой сочетание различных геометрических тел или их частей. Следовательно, для чтения и выполнения чертежей нужно знать, как изображаются геометрические тела в системе трех проекций на производстве (табл. 7). (Чертежи, содержащие три проекции, называются ком­плексными чертежами.)

7. Комплексные и производственные чертежи деталей простой геометрической формы

П p и м e ч а н и я: 1. В зависимости от особенностей производственно­го процесса на чертеже изображают определенное число проекций. 2. На чертежах принято давать наименьшее, но достаточное число изо­бражений для определения формы предмета. Число изображений чер­тежа можно уменьшить, используя условные знаки s, l, ? которых вы уже знаете.

Частный случаем пересечения плоскостей являются взаимно перпендикулярные плоскости.

Известно, что две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой. Через точку А можно провести множество плоскостей, перпендикулярных данной плоскости a ( h , f ) . Эти плоскости образуют в пространстве пучок плоскостей, осью которого является перпендикуляр опущенный из точки А на плоскость a . Для того, чтобы через точку А провести плоскость, перпендикулярную плоскости a ( h ,f ) , необходимо из точки А провести прямую n, перпендикулярную плоскости a ( h ,f ) , (горизонтальная проекция n 1 перпендикулярна горизонтальной проекции горизонтали h 1 , фронтальная проекция n 2 перпендикулярна фронтальной проекции фронтали f 2 ). Любая плоскость, проходящая через прямую n a ( h ,f ) , поэтому для задания плоскости через точку А проводим произвольную прямую m . Плоскость заданная двумя пересекающимися прямыми (m ,n) , будет перпендикулярна плоскости a ( h ,f ) (рис. 50).

3.5. Отображение относительного положения прямой и плоскости

Известны три варианта взаимного расположения прямой и плоскости:

Прямая принадлежит плоскости.

Прямая параллельна плоскости.

Прямая пересекает плоскость.

Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.

Большое значение для задач начертательной геометрии имеет частный случай пересечения прямой и плоскости, когда прямая перпендикулярна плоскости.

3.5.1. Параллельность прямой и плоскости

При решении вопроса о параллельности прямой линии и плоскости необходимо опираться на известное положение стереометрии: прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости и не принадлежит этой плоскости.

Пусть дана плоскость общего положения ABC и прямая общего положения а. Требуется оценить их взаимное положение (рис. 51).

Для этого через прямую а проведем вспомогательную секущую плоскость g - в данном случае горизонтально проецирующая плоскость. Найдем линию пересечения плоскостейg и А ВС - прямую п (DF ). Проекция прямой п на горизонтальную плоскость проекций совпадает с проекцией а 1 и со следом плоскости g . Проекция прямой п 2 параллельна а 2 , п 3 параллельна а 3 , следовательно, прямая а параллельна плоскости AВС.

3.5.2. Пересечение прямой с плоскостью

Нахождение точки пересечения прямой линии и плоскости – одна из основных задач начертательной геометрии.

Пусть дана плоскость AВС и прямая а. Требуется найти точку пересечения прямой с плоскостью и определить видимость прямой по отношению к плоскости.

Алгоритм решения задачи (рис. 52) следующий:

Через горизонтальную проекцию прямой а 1 проведем вспомогательную горизонтально проецирующую плоскость g .

Находим линию пересечения вспомогательной плоскости с заданной. Горизонтальный след плоскости g 1 пересекает проекцию плоскости A 1 В 1 С 1 в точках D 1 и F 1 , которые определяют положение горизонтальной проекции п 1 - линии пересечения плоскостей g и AВС . Для нахождения фронтальной и профильной проекции п спроецируем точки D и F на фронтальную и профильную плоскости проекций.

Определяем точку пересечения прямых а и п. На фронтальной и профильной проекциях линия пересечения плоскостей п пересекает проекции а в точке К , которая и является проекцией точки пересечения прямой а с плоскостью AВС , по линии связи находим горизонтальную проекцию К 1 .

Методом конкурирующих точек определяем видимость прямой а по отношению к плоскости AВС .

Задача № 1.

Построить комплексный чертеж точки А, если:

точка расположена во II четверти и равноудалена от плоскостей  1 и  2 .

точка расположена в III четверти, и ее расстояние до плоскости  1 в два раза больше, чем до плоскости  2.

точка расположена в IV четверти, и ее расстояние до плоскости  1 больше, чем до плоскости  2 .

Задача № 2.

Определить, в каких четвертях расположены точки (рис. 2.21).

Задача № 3.

Построить наглядное изображение точек в четвертях:

а) А – общего положения в III четверти;

б) В – общего положения в IV четверти;

в) С – во второй четверти, если ее расстояние от  1 равно 0;

г) D – в I четверти, если ее расстояние от  2 равно 0.

Задача № 4.

Построить комплексный чертеж точек А, В, С, D (см. задачу 3).

§ 5. Система трех взаимно перпендикулярных плоскостей

На практике исследования и построения изображений система двух взаимно перпендикулярных плоскостей не всегда дает возможность однозначного решения. Так, например, если переместить точку А вдоль оси Х, то ее изображение не изменится.

Положение точки в пространстве (рис. 2.22) изменилось (рис. 2.24), а изображения на комплексном чертеже остались без изменений (рис. 2.23 и рис. 2.25).

Для решения данной задачи вводят систему трех взаимно перпендикулярных плоскостей, так как при составлении чертежей, например машин и их частей, требуется не два, а больше изображений. На этом основании в некоторые построения при решении задач необходимо вводить в систему  1 ,  2 и другие плоскости проекций.

Эти плоскости делят все пространство на VIII частей, которые называются октантами (от лат. okto восемь). Плоскости не имеют толщины, непрозрачны и бесконечны. Наблюдатель находится в первой четверти (для систем  1 ,  2) или первого октанта (для систем  1 ,  2 ,  3) в бесконечном удалении от плоскостей проекций.

Главная » База знаний » Черчение. Система трех взаимно перпендикулярных плоскостей 3 взаимно перпендикулярные плоскости